[생화학I] 8. Hill equation으로 미오글로빈 해석하기

앞선 글에서 미오글로빈과 헤모글로빈이 무엇인지, 산소운반을 가능케 하는 Heme이 무엇인지를 살펴보았다. 그러면 이들이 실제 체내에서 어떻게 작동하는지를 알아보자. 처음부터 헤모글로빈을 다루기에는 복잡하니, 간단한 미오글로빈부터 다뤄보자. 
 

Hill equation을 구해보자

Hill equation은 단백질-리간드 결합 모델을 해석하기 위한 방정식이다. 미오글로빈 또한 단백질의 일종이니 Hill equation을 통해 해석할 수 있다. 참고로 미오글로빈은 단량체이다. 즉 하나의 Heme을 가지고 있으며, 하나의 미오글로빈은 하나의 산소와만 결합할 수 있다. 이를 Single Ligand binding Site를 가졌다고 한다. 그래서 앞으로 구하려고 하는 Hill equation은 Single Ligand binding site를 가지는 단백질의 경우에 적용되는 식이다. 참고로 미오글로빈 외에도 보편적으로 적용되는 식을 먼저 구한 뒤 미오글로빈의 상황으로 전환하겠다. 

유도과정 1

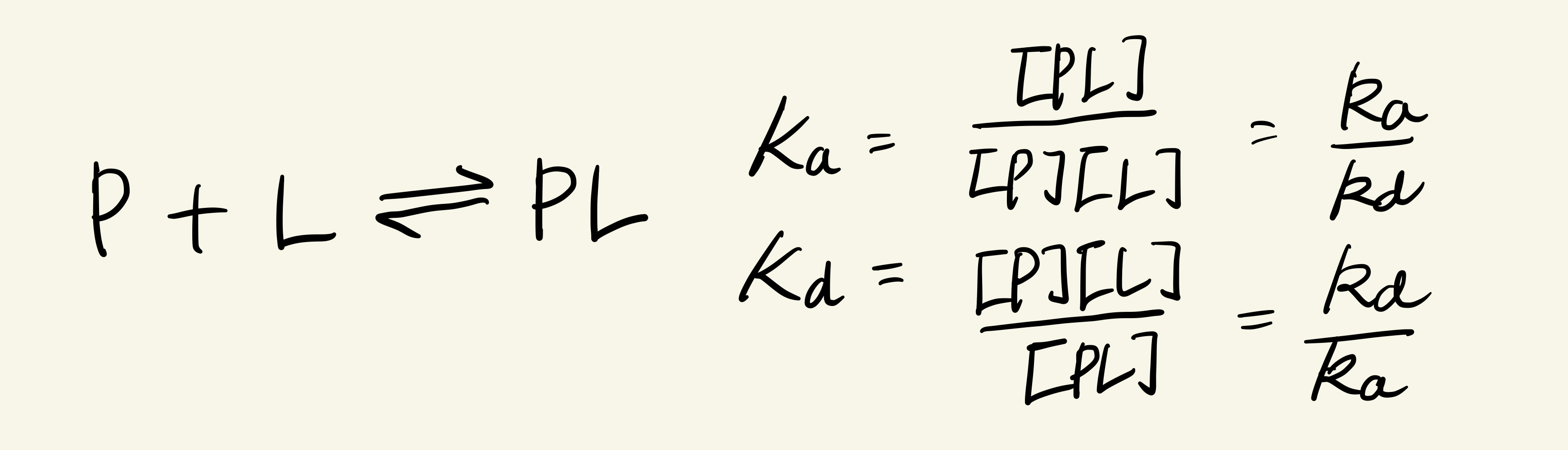
우선 P는 단백질이며, L은 리간드를 의미한다. PL은 단백질과 리간드가 결합하여 만들어진 복합체이다. 이때, 리간드의 결합은 가역적인 반응으로, 단백질과 리간드가 결합하여 복합체를 이룰수도 있으며 반대로 복합체에서 단백질과 리간드로 분리될수도 있다. 대문자 K는 평형상수를 의미한 것이며, 소문자 k는 속도 상수이다. a는 정반응일 때이며, d는 역반응일 때를 의미한다. 
 
Single Ligand binding site를 가진 단백질은 위와 같은 평형 상태에 있다고 가정할 수 있으며, 이때 평형 상수를 정의할 수 있다. Ka가 클수록 PL이 더 많이 형성되는 쪽으로 평형이 이뤄지므로, 단백질의 리간드에 대한 친화도(Affinity)가 더 크다고 판단할 수 있다.

유도과정 2

이제 θ를 정의해보자. θ는 전체 단백질 중 리간드와 결합해서 포화된 단백질의 비중을 의미한다. 쉽게 말해서 포화도(Fractional saturation)이다. 우선 분모로 온 [PL]+[P]는 리간드와 결합한 단백질과 결합하지 않은 단백질의 합, 즉 존재하는 모든 단백질을 의미한다. [PL]+[P]에 대한 [PL]의 비율이니 가용한 모든 단백질 중 리간드와 결합한 단백질의 비율로 해석할 수 있겠다. 유도과정1에서 정반응 평형상수 Ka를 정의했었다. 이 식을 [PL]에 대해 바꿔서 대입하면 유도과정2의 마지막처럼 식을 정리할 수 있다.

유도과정 3

유도과정2에서 얻은 식을 Ka[P]로 나눠주면 유도과정3의 첫번째 식이 된다. Ka[P]가 0이 되는 경우는 무의미한 경우니 무시하고 그냥 나눠줘도 된다. Ka의 역수는 곧 유도과정1의 정의에 따라 Kd와 동치이므로 Kd로 대체하여 유도과정3의 마지막 식을 얻을 수 있다. 

 
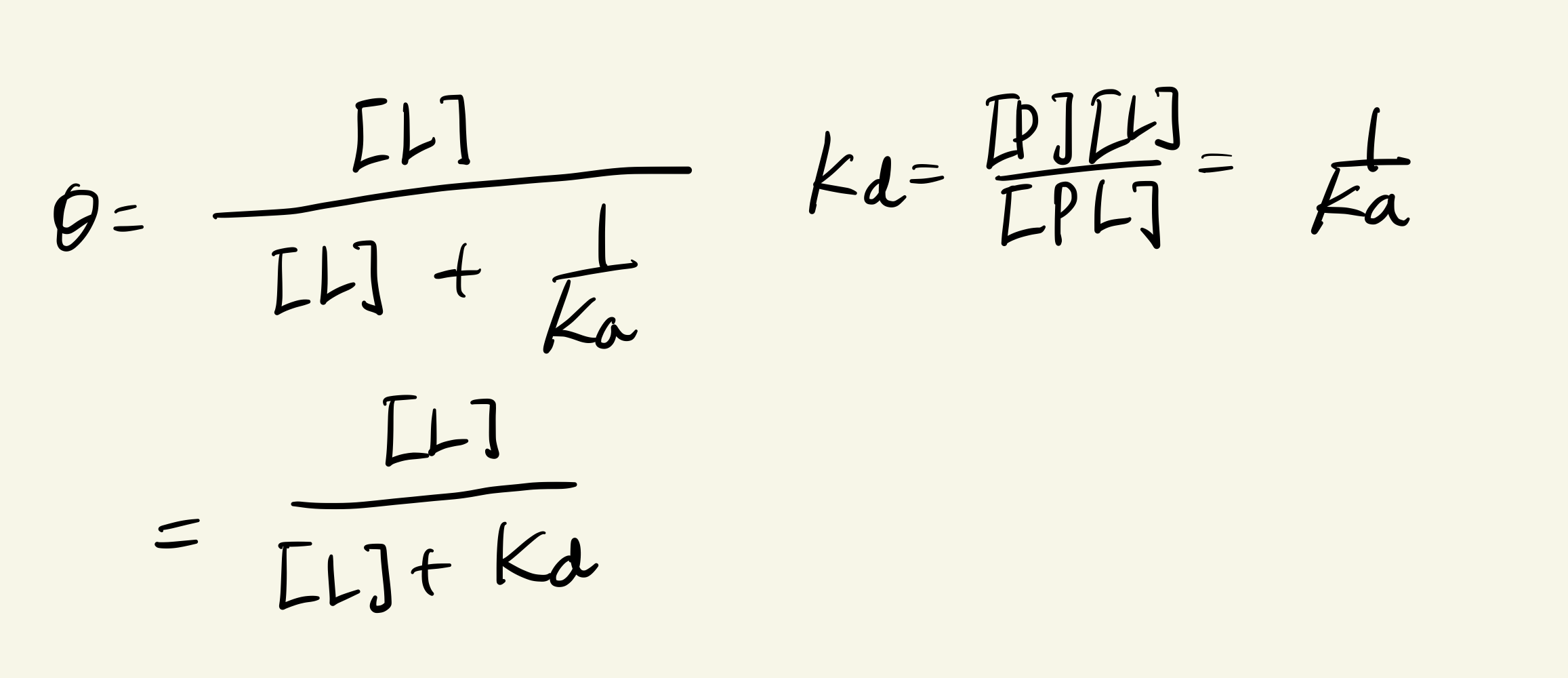
그러면 이제 미오글로빈의 경우에 적용해보자. 미오글로빈의 경우는 산소와 결합하는 단백질이니 리간드로 산소가 온다. 즉 [L]을 [O2]로 바꿔서 생각할 수 있다. 하지만 혈액에 녹아있는 직접적인 농도를 측정하는 것보다는 분압을 측정하는 것이 더 쉽기 때문에 [O2] 대신 pO2를 통해 리간드를 표현하게 된다. 
 

유도과정 4

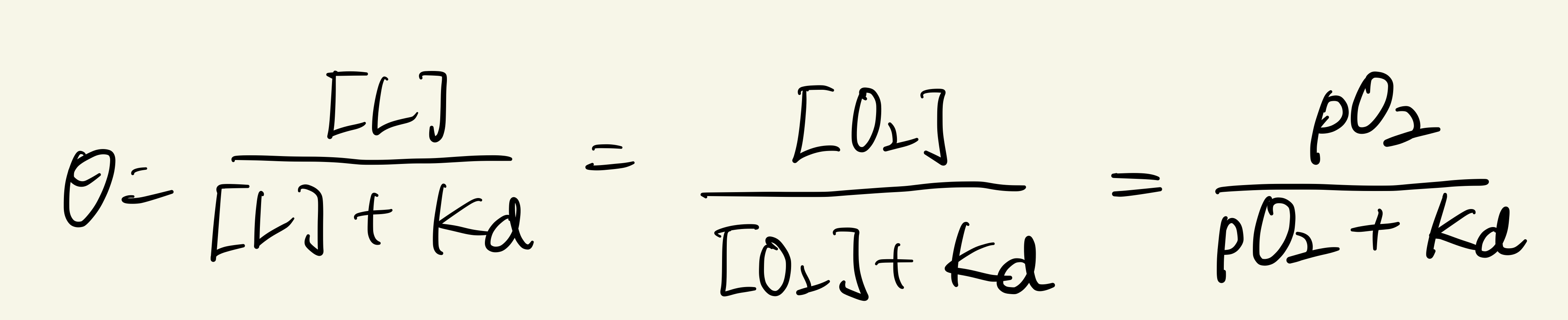
여기서 Kd는 가능한 리간드 결합 가능 구역 중 절반이 차있을 때의 리간드 농도와 같다고 알려져 있다. 미오글로빈에서 리간드는 산소이므로, 모든 미오글로빈이 산소로 포화되었을 때에서의 산소 농도를 반으로 나누면 곧 Kd가 된다. (Kd=0.5[L]=0.5[O2]) 위에서 산소의 농도를 직접 사용하지 않고 분압을 활용해서 식을 표현한다고 밝힌 바 있다. 따라서 Kd 또한 분압의 형태로 바꿔주도록 하자. 여기서 정의되는 게 P50인데, 미오글로빈의 절반이 포화될 때의 산소 분압이 된다.

유도과정 5

Kd와 P50의 개념을 확인해보자

위 그림에서 θ=0.5가 될 때 가로축에 오는 값이 Kd 또는 P50으로 정의가 된다. 

 

미오글로빈에서의 Hill equation

미오글로빈의 경우, 포화도를 나타낼 때는 θ를 대신해서 보통 YO2로 표현을 하곤 한다. 이때의 식이 미오글로빈에서의 Hill equation이 된다. 만약 이를 그래프로 그릴 경우, Hyperbolic한 형태로 그려진다. (만약 Hyperbolic 형태가 궁금하면 유도과정 5 그림 다음에 있는 그림을 참고해보자) 이 경우는 우리가 해석하기 불편한 점이 있기 때문에 식을 다르게 접근해서 형태로 바꿔주도록 하자. 

추가 유도과정 1

YO2가 포화도를 나타낸 것이면 1-YO2는 비포화도가 된다. 이를 활용해서 새로 식을 세워서 우변을 아주 간단하게 정리해줬다.

추가 유도과정 2

이 상태에서 양변에 로그를 씌워주면 식이 y=x+b의 일차함수 꼴이 된다. (로그는 밑이 10인 로그로 생각하자) 즉 일차함수처럼 그래프가 Linear하게 나타나서 해석하기 더 쉬워진다. 이때 y에 해당하는 것은 log(YO2/(1-YO2)), x에 해당하는 것은 log(PO2), b에 해당하는 것은 -log(P50)이다. 이를 통해 우리는 아래의 변환된 형태의 Hill equation을 얻었다.

미오글로빈의 Hill equation을 변환한 형태

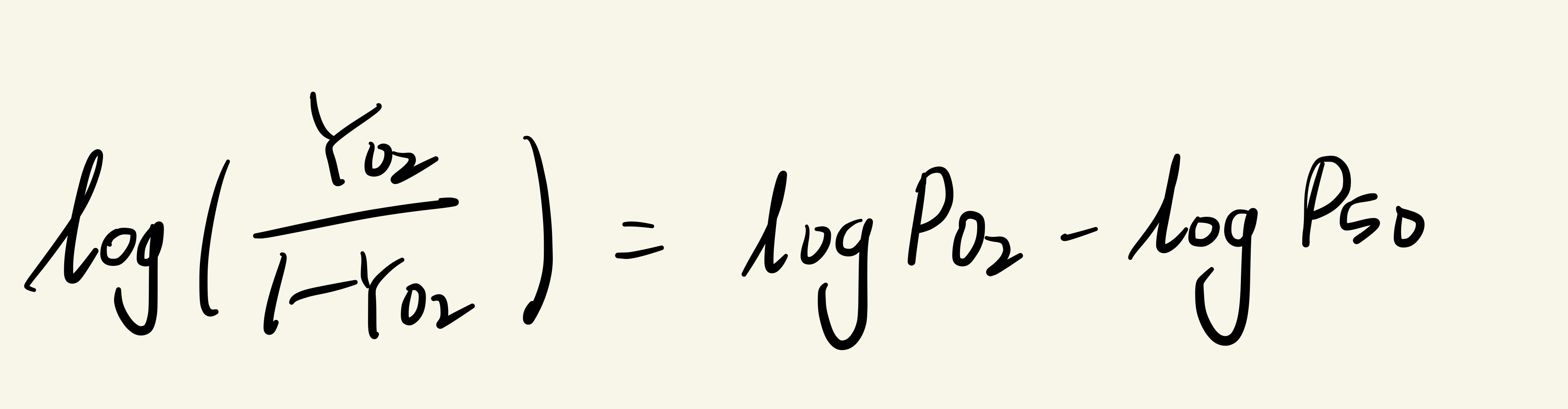
이제 두 식을 모두 배웠으니 두 식을 그래프 상에 나타냈을 때 어떻게 나타나는지 실제로 한번 확인해보자.
 
아래 두 그림에서 같은 색(남색, 하늘색, 붉은색)으로 나와있는 그래프는 서로 같은 미오글로빈을 나타낸 것이다. 또 아래 경우에서는 미오글로빈의 산소 친화도가 서로 다르다고 가정하고 그래프를 그린 것이다.

• 남색: YO2=PO2/(3+PO2)
• 하늘색: YO2=PO2/(16+PO2)
• 붉은색: YO2=PO2/(44+PO2)

우선 상수인 3, 16, 44에 해당하는 것이 P50, 즉 미오글로빈의 절반이 산소로 포화되었을 때의 산소 분압이다. 이 수치가 작을수록 미오글로빈의 산소에 대한 친화도가 높다고 판단할 수 있다. (적은 산소로도 미오글로빈이 산소로 많이 포화되기 때문) Hyperbolic 형태로 나타냈을 때 세로축의 YO2는 포화도이므로 0부터 1까지의 범위를 가진다. 그래서 붉은색이나 하늘색으로 나타난 그래프도 PO2가 계속해서 증가하다보면 언젠가는 1에 가깝게 도달한다. 다만 여기서는 공간이 부족해서 생략된 것이라 할 수 있다. 

Hyperbolic 형태로 그려진 그래프

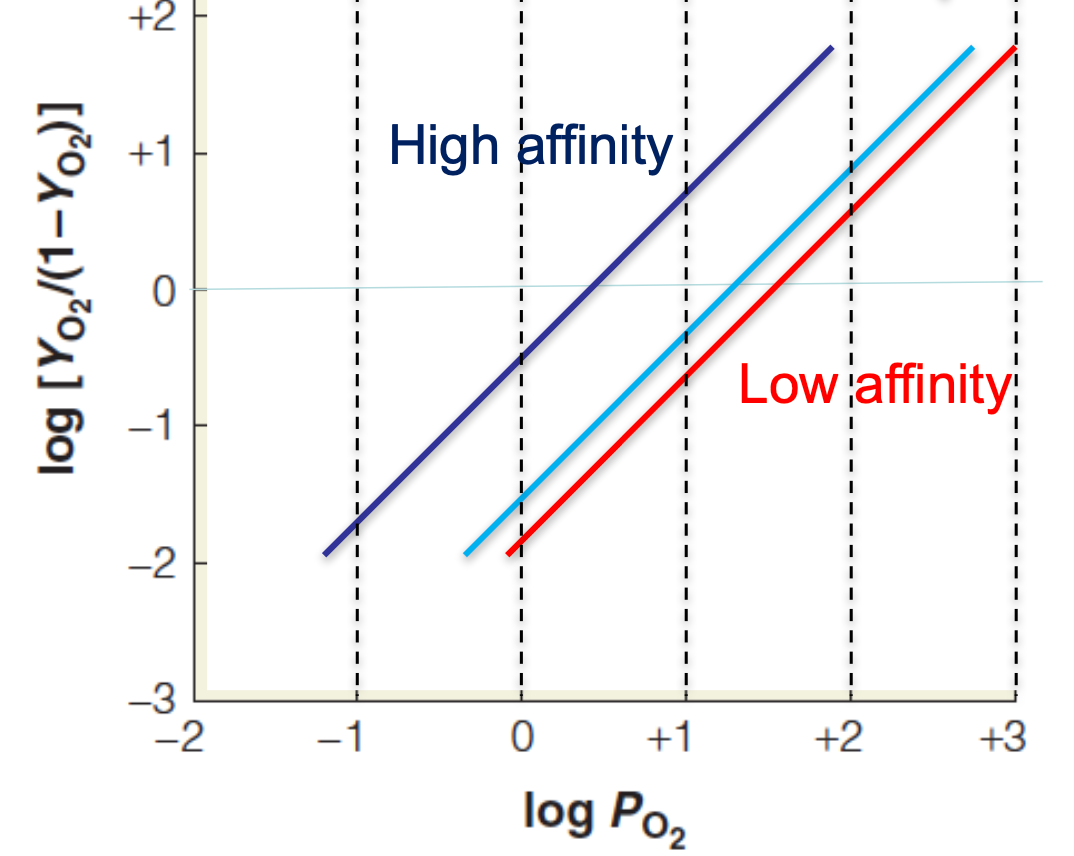
다음은 Linear 형태로 나타낸 경우이다. 세로축에 나와있는 log(YO2/(1-YO2))의 값은 미오글로빈의 상황에 따라서 달라진다. 만약 산소로 포화된 미오글로빈과 그렇지 않은 미오글로빈의 양이 같을 경우(YO2=1-YO2=0.5), YO2/(1-YO2)=1이 되므로, 로그를 씌웠을 때 그 값이 0이 된다. 이를 기준으로 해서 로그값이 양수일 경우, 산소와 결합한 미오글로빈이 더 우세하여 YO2/(1-YO2)가 1보다 커졌음을 알 수 있다. 반대로 로그값이 음수일 경우, 산소와 결합하지 않은 미오글로빈이 더 우세하여 YO2/(1-YO2)가 1보다 작아졌음을 알 수 있다. 
 
그래서 log(PO2)에 따라 그래프가 양수인지, 음수인지, 아니면 0에 위치하는지 단순히 비교함으로써 미오글로빈이 해당 분압에서 어떤 상황에 있는지 쉽게 판단할 수가 있다. 

Linear 형태로 그려진 그래프

 
물론 Hyperbolic 형태이든, Linear 형태이든 아직까지는 크게 차이를 못 느낄 수도 있다. 미오글로빈의 경우는 단순한 편이기 때문에 두 그래프 모두 해석하는 데 큰 어려움이 있지 않다. 다음 글에서 헤모글로빈과 Allosteric effect을 알아본 뒤, 미오글로빈과 어떤 점이 다른지 비교해보는 것도 좋을 것 같다.